An alternative approach to Pre-Algebra, Algebra 1, or Algebra 2!
An alternative approach to Pre-Algebra, Algebra 1, or Algebra 2!
The reason that we named our program “Algebra: A Complete Course,” is that we believe the best way to learn Algebra is to start at the beginning and end at the end! In this program you will find a complete study of the essential material covered in a traditional Algebra 1 and Algebra 2 course.
However, we need to continue a little further with this answer because Algebra 1 and Algebra 2 are terms that refer mostly to the traditional way that Algebra has been taught. Traditional Algebra 1 classes attempt to cover most of Algebra in the first year, but the methods that are used, and the speed with which the material is covered, hinders student understanding of the material. Instead, the student is just exposed to memorizing rules, formulas, tricks, and shortcuts. By the time they get to what is called an Algebra 2 course, (sometimes after they take a Geometry course), they have forgotten almost all of the Algebra that they memorized. So, that Algebra 2 course (which is by definition, a rehash of whatever has been called “Algebra 1”), must repeat practically all of the Algebra 1 course. In fact, it usually repeats a lot of the Pre-Algebra material as well. This is usually referred to as the “spiral method” of learning, and it is not very effective in helping students to excel, especially at this level of mathematics.
We think that this huge overlap is generally unproductive, and largely unnecessary if the concepts are taught analytically. Therefore we call our program “Algebra: A Complete Course,” because we employ a mastery-learning approach, sometimes moving at a slower pace, but without the overlap. As a result, students often complete the course even more quickly.
PROGRAM DESCRIPTION:
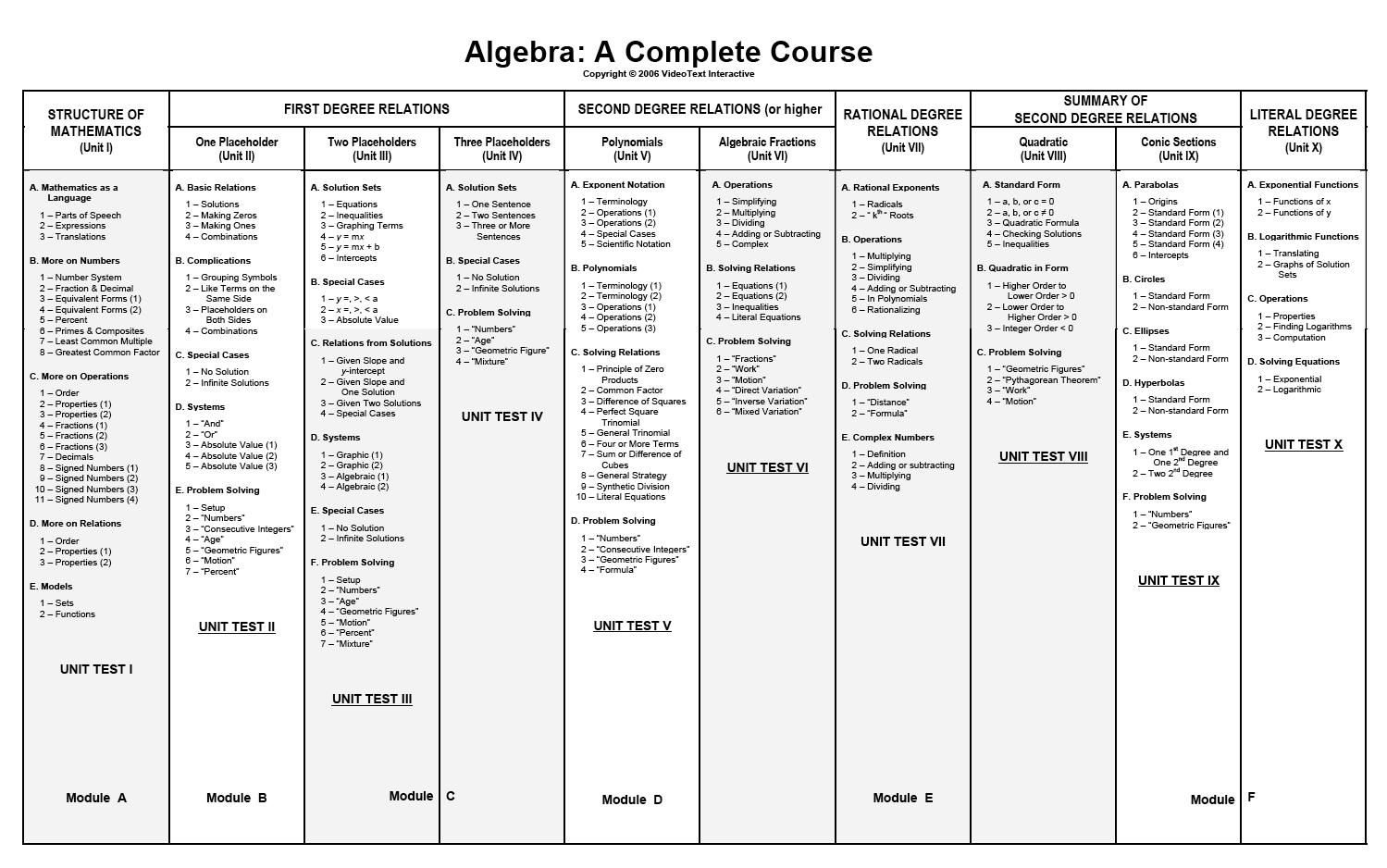
There are 176 video lessons contained in 10 unit directories. The program covers Pre-Algebra, Algebra I and Algebra II, and is a firm foundation for students advancing to VideoText’s Geometry: A Complete Course, covering Geometry and Trigonometry. Each Algebra Program Module includes DVDs and corresponding books (Course Notes, Student WorkText, Solutions Manual, Instructor’s Guide and Progress Tests).
Materials in the complete course include:
176 Video Lessons – Each of the 5-10 minute lessons explore Algebra concepts in a detailed logical order. Because no shortcuts or tricks are used, the methods are easy to follow and promote clear understanding.
360 pages of Course Notes – These notes allow students to review the logical development of a concept. Each page chronologically follows the video lesson, repeating exactly what was shown on the screen.
590 pages of Student WorkText – These pages review the concept developed in each lesson. More examples are given and exercises are provided for students. The explanations are virtually free of complicated language, making it easy for students to follow the logic of each concept.
Solutions Manuals – These manuals provide detailed, step-by-step solutions for every problem in the student WorkText. This resource is a powerful tool when used by students to complete an error-analysis of their work, and to check their thought processes.
Progress Tests – These tests, with the step-by-step answer keys (Instructor’s Guides) included, are designed to have students demonstrate understanding, lesson-by-lesson, and unit-by-unit. There are two versions of each test, allowing for retesting or review, to make sure students have mastered concepts.
CLAIMED CREDITS:
When a student completes Algebra: A Complete Course, the student can claim credits for all of the following:
- Algebra I (1)
- Algebra II (1)
With the completion of Geometry: A Complete Course, the student can also claim credits for:
- Geometry (1)
ALGEBRA PROGRAM OVERVIEW:
The VideoText Algebra program addresses two of the most important aspects of mathematics instruction. First, the inquiry-based video format contributes to the engaging of students more personally in the concept development process. Through the frequent use of the pause button, you, as the instructor, can virtually require interaction and dialogue on the part of your student. As well, students who work on their own, can “simulate” having an instructor present by pausing the tape every time a question is asked and trying to answer it correctly before continuing. Second, each incremental concept is explored in detail, using no shortcuts, tricks, rules, or formulas, and no step in the process in ignored. As such, the logic and the continuity of the development assures students that they understand completely. Subsequently, learning is more efficient, and all of the required concepts (topics) of the subject can be covered with mastery. Of course, the benefits of these efforts can be seen even more clearly in a description of a typical session as follows:
After a brief 2 or 3 sentence introduction of the concept to be considered, usually by examining the description and the objective given at the beginning of the video lesson, you and your student can begin. You should pause the DVD frequently, usually every 15-20 seconds (or more often if appropriate), to engage your student in discussion. This means that for a 5- 10 minute VideoText lesson, it may take 15-20 minutes to finish developing the concept. Dialogue is a cornerstone. In addition, during this time, your student should probably not be allowed to take notes. He or she must not have their attention divided, or they risk missing important links. Neither should you be dividing your attention by looking at notes or writing on a note pad or an overhead projector. Everyone is concentrating on concept development and understanding. Please understand that a student who is accustomed to working alone, or can be motivated to study independently, has, with the VideoText, a powerful resource to explore and master mathematical concepts by simulating the dialogue normally encountered with a “live” instructor. And, because of the extensive detail of the explanations along with the computer generated graphics and animation, students are never shortchanged when it comes to the insight necessary to fully comprehend.
Once the concept is developed and the VideoText lesson is completed, you can then employ the course notes to review, reinforce, or to check on your student’s comprehension. These course notes are exact replications of the content that was viewed in the VideoText lesson, illustrating the same terms, problems, numbers, and. logical sequences. In fact, at this time, if your student needs a little more help, he or she can use these course notes while viewing the lesson again, using them as a guide through the reexamination of the concept. .The key here is that students concentrate on understanding first, and take care of documentation later.
Please understand that the goal of VideoText videos are not to necessarily replace an “instructor”, but rather to help aid in prompting students to actively engage in the instruction process. The video should never tell your student anything that hasn’t been considered or discussed (while the DVD is paused), and it should never answer questions that have not already been resolved. As such, it becomes a “new breed of overhead projector whereby you, as the teacher, or your student working alone, can “write” on this overhead simply by pressing the “play” button. This is a critical point to be understood and should serve to help you examine all of the materials and strategies from the proper perspective.
Finally, your student can begin to do some work independently, either by your introduction of additional examples from the WorkText, or by the student immediately going to the WorkText on his or her own. The primary feature of the WorkText, beside providing problem banks with which students can work on mastery, is that objectives are restated, important terms are reviewed, and additional example are considered, in noticeable detail, taking students, once again, through the logic of the concept development process. The premise here is simple. When students work with an instructor, whether doing exercises on their own or working through them with other students, they are concentrating more on “how to do” the problems. Then, when they leave the instructor, they simply don’t take the discussion of the concept with them. The goal of the program is to provide a resource which will help students “relive” the concept development on their own, whether for review or for additional help. That is the focus of the Student WorkText.
In addition, there are detailed Solutions Manuals, which afford the opportunity to check work and engage in error analysis. Of course, there are also quizzes, unit tests, cumulative reviews, and final examinations to help you to further assess your student’s progress. In fact, the assessment package often utilizes open-response questions which require the learners to state, in writing, their understanding of the concept. This often reveals much more about a student’s understanding of a concept than just checking to see if an answer on a test is correct.
As you can see, the highly interactive quality of this program, at a personal level, affords students a much greater opportunity than usual to grow mathematically and develop confidence in their ability. As well, they can review the video lessons as often as they wish to further ground that understanding.
ALGEBRA SCOPE AND SEQUENCE RATIONAL:
There are two basic premises which drive concept development in Algebra, and these two essentials shape the logical scope and sequence of algebraic content. First, it is generally understood that the study of Algebra is the study of relations. In the same way that Geometry focuses on spatial concepts, and Calculus is concerned with rates of change, Algebra is a comprehensive exploration of mathematical relationships, including both equations and inequalities. As such, no treatment of Algebra should ever separate equations from inequalities, especially when it utilizes a format which addresses them in different “chapters.” In fact, a true adherence to the National Council of Teachers of mathematics (NCTM) standards, requires us to deal specifically with functions, and we know that the set of functions is a subset of the set of relations, without regard initially to the differences between equations and inequalities. Therefore, in this course, equations and inequalities are studied together, and distinctions are made only when necessary, to clarify functional differences. As an aside, documentation exists to show that students generally have little or no trouble working with all types of relations at the same time and, in fact, understand the logic of studying them together.
The second premise is that the concepts of Algebra develop by degrees. This means, of course, that relations of first-degree should be mastered first. In fact, as instructors, we all understand that relations of any degree other than one must be “reduced” to relations of first-degree, or “factored” into linear or first-degree factors, before they can be resolved. The impact of this understanding on the scope and sequence of Algebra content, is to organize the various types of relations, by degree. In this course, first-degree relations are examined exhaustively before higher-order relations are encountered. Unit II deals with first-degree relations with one variable. Unit III then addresses first-degree relations with two variables. Unit IV considers first-degree relations with three or more variables. The idea here is to help students master first-degree relations, before moving on to relations of other degrees (or orders). This is not only more mathematically correct than the traditional treatment, but it allows students to reinforce more efficiently, one-variable concepts by immediately moving to two-variable concepts, and then to concepts involving three or more variables. And we all know that a system of relations with three variables is resolved using the same approach as a system with only two variables.
Moving on to Unit V, students quickly review exponent notation, including the various properties of powers and operations with powers, and investigate relations with integral degrees of 2 or higher. Unit VI continues this exploration with a focus on algebraic fractions, in which negative, integral exponents make a prominent appearance. In Unit VII, fractional exponents are introduced, which obviously pave the way for a study of radicals and roots. This, of course, is the seed from which rational-degree relations develop, or, as they are more commonly called, relations with radicals in them.
Then, after a review of second-degree relations with one variable (Unit VIII – The Quadratic Relations) and two variables (Unit IX – The Conic Sections), the study of Algebra is completed by examining the only type of exponent not yet investigated – the variable, or placeholder. This is the start of a study of literal-degree relations, and is the basis for the development of exponential and logarithmic functions. It is only after considering all possible degrees, that we can say we have studied a complete course in Algebra. In that context, it is quite artificial to define, for everyone, what “Algebra 1” is, or “Algebra 2”, or even “Pre-Algebra”.
The logical scope of Algebra covers relations of all degrees, including numeric and literal, while the sequence of concepts begins with a mastery of first-degree relations and grows systematically to include increasingly more sophisticated degrees. One more organizational quality is noteworthy here. The normal flow of each unit is based on the logical introduction of any new mathematical symbolism. First, the new “thing” is defined and described in detail. Then, operations involving the new “thing” are explored. Finally, relations involving this new “thing” are examined, and strategies are developed to resolve them. This cycle is introduced and explained in Unit I, and is evidenced in each successive unit. For example, in Unit V, polynomials are introduced. This is new mathematical symbolism for the student, and it must be defined carefully. Then, operations with polynomials must be examined. All of this culminates, of course, in learning to solve relations with polynomials. This logical cycle of exploration in mathematics is helpful to students, providing them with some anticipation of the levels of exploration necessary to develop algebraic concepts. Please understand that the organizational argument presented here is not meant to stifle the creativity of the instructor. Neither should it prohibit the instructor from utilizing a modular approach to concept development. It does, however, serve to remedy the fragmented, isolated topic, “chapter” approach, to a subject which has been traditionally presented to us in “textbooks”, without that element of developmental continuity. To that end, it speaks loudly to the curricular issues which all instructors face, and the attitudinal issues students deal with when they are presented with the fact that “everyone must pass Algebra”.